Odds Ratios And Log Odds Ratios Clearly Explained Youtube
This StatQuest covers those subjects so that you can understand the stati Risk ratios, odds ratios, and hazard ratios are three ubiquitous statistical measures in clinical research, yet are often misused or misunderstood in their interpretation of a study's results A 01 paper looking at the use of odds ratios in obstetrics and gynecology research reported 26% of studies (N = 151) misinterpreted odds ratios as risk ratios , while a 12 paper
Convert log odds to odds ratio
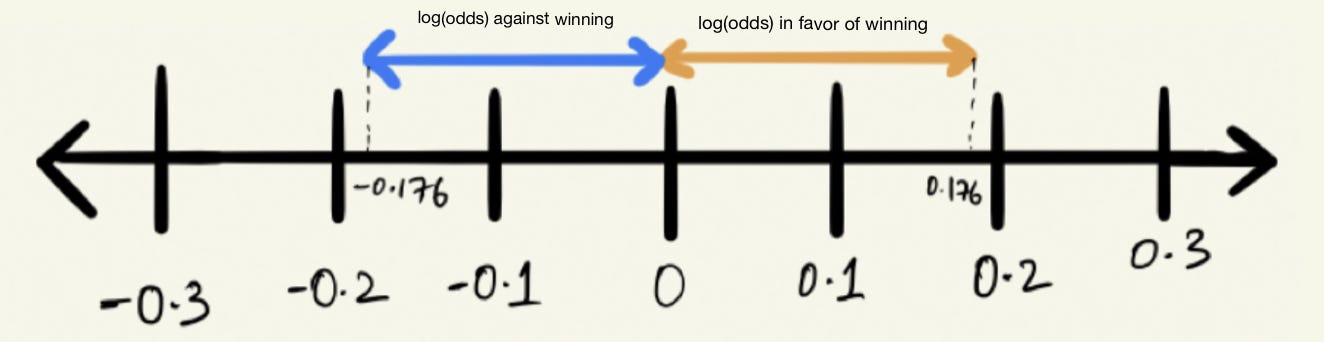
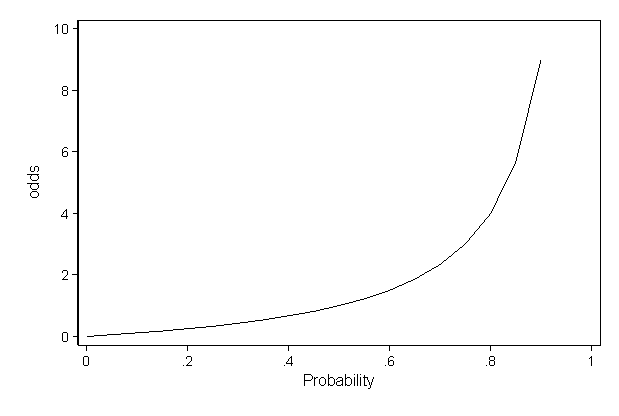
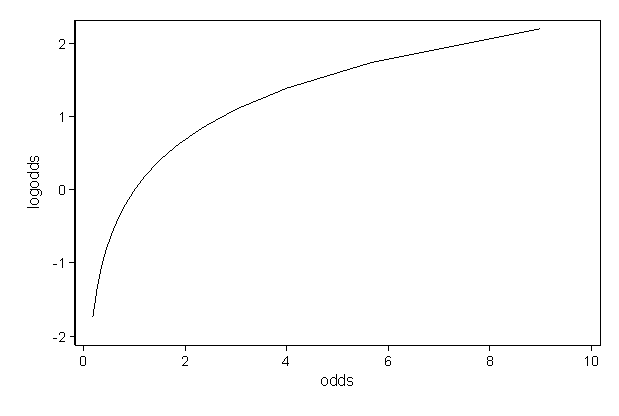
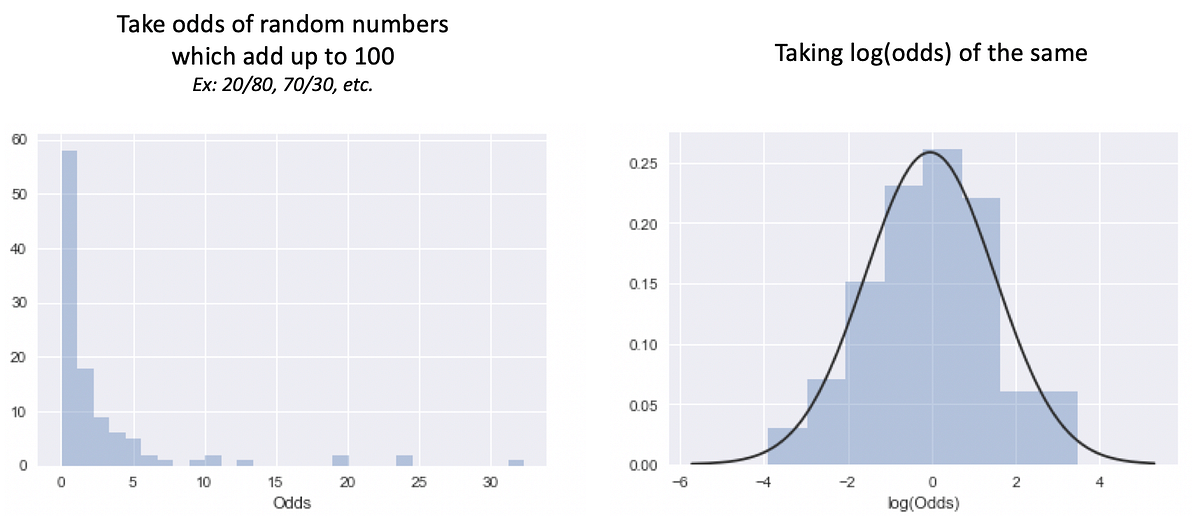
Convert log odds to odds ratio-Log_odds = seq(from =5,to =5,by =025) odds = exp(log_odds) # use 'plogis' function to calculate exp(x)/(1 exp(x)) p = plogis(log_odds) # use odds/(1odds) to calculate p a different way p2 =odds/(1odds) # store probability of failure (1p) q =1p # store log_odds and y in data frame for use with ggplot 1 log (Odds of losing) = log (15) = 0176 Figure6 log (odds) on a Number Line Look at that, it looks so symmetrical and a fair comparison scale now So basically using the log function helped us making the distance from origin (0) same for both odds, ie, winning (favor) and losing (against)

Log Odds Ratio Plot Of Tnt Vs Diagnoses Download Scientific Diagram
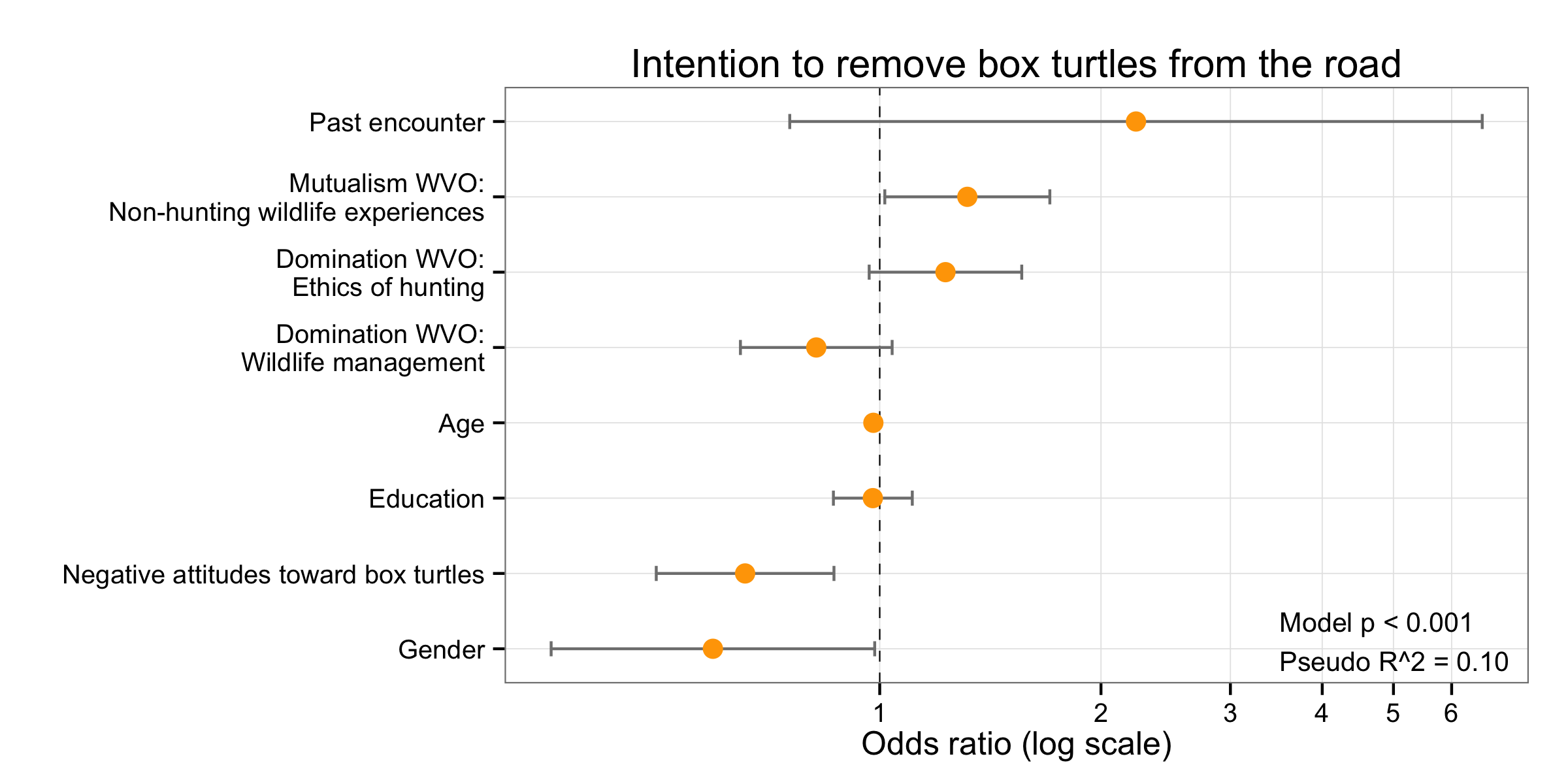
The odds ratio for your coefficient is the increase in odds above this value of the intercept when you add one whole x value (ie x=1; SE of Beta You can calculate the upper and lower bounds for the OR by Upper bound = OR se (OR) x 196 Lower bound = OR se (OR) x 196 Log (upper bound of OR) = upper bound of beta Log 1 The logistic regression coefficient indicates how the LOG of the odds ratio changes with a 1unit change in the explanatory variable;
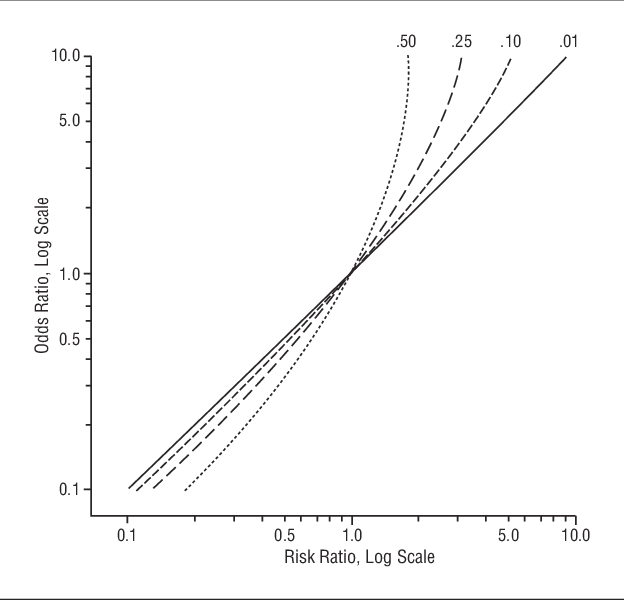
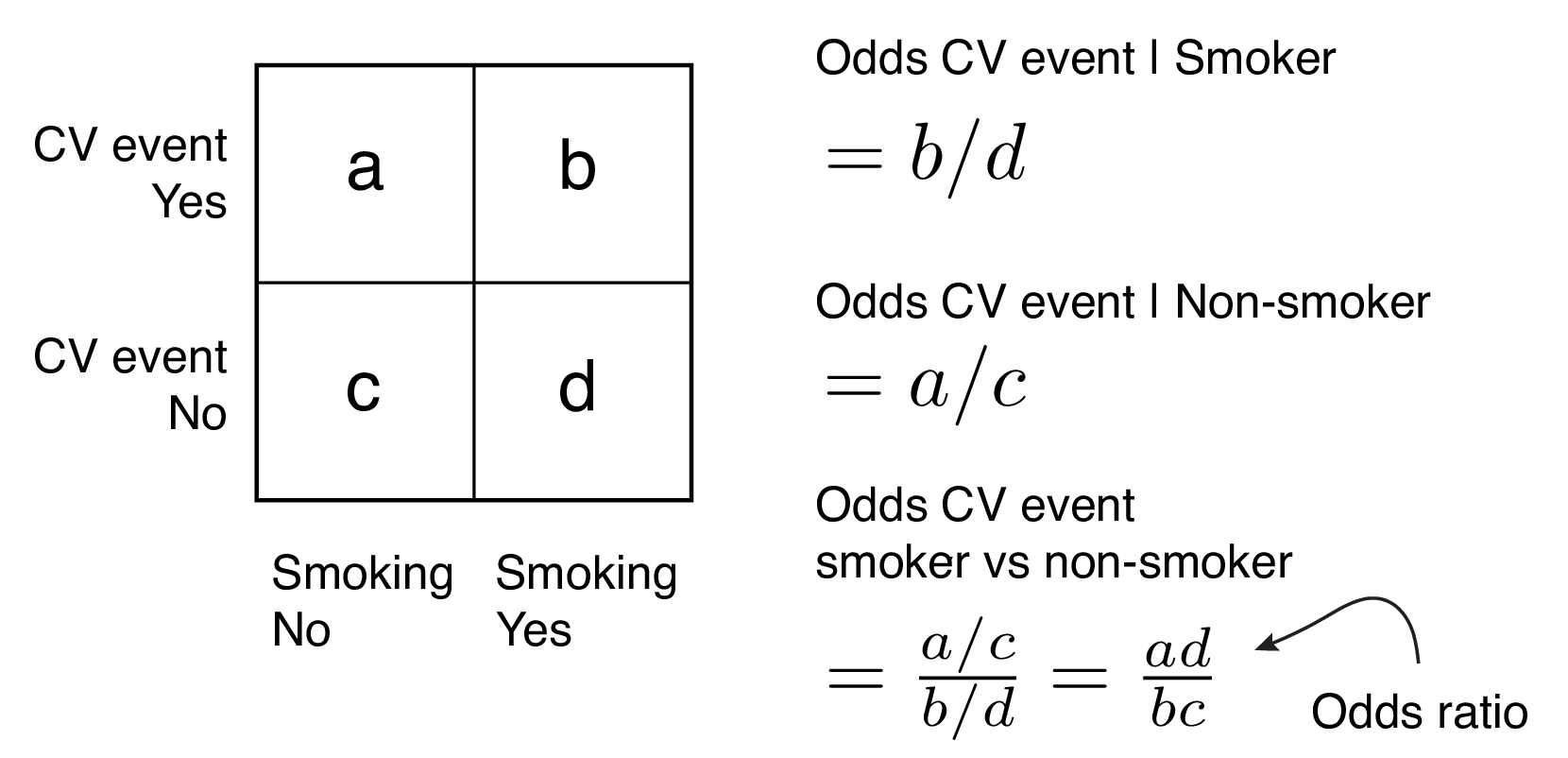
Odds ratios (OR) are commonly reported in the medical literature as the measure of association between exposure and outcome However, it is relative risk that people more intuitively understand as a measure of association Relative risk can be directly determined in a cohort study by calculating a risk ratio (RR) e x p ( β) = odds ratio = p 1 1 − p 1 p 2 1 − p 2 I guess what's not coming across is how β, not being a ratio of odds, converts to the odds ratio metric, when taken out of logarithmic space To provide a bit more, if this is the logistic regression equation for the constant l o g ( p 1 − p) = β β 1 ∗ 0 β 2 ∗ 0 β 3 ∗ 0 β 4 ∗ 0 β 5 ∗ 0 then e x p ( β) = odds ratioInstead, any estimated odds ratio is conditional on the data and the model specification Odds ratios should not be compared across different studies using different samples from different populations
Convert log odds to odds ratioのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Convert log odds to odds ratio」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
Odds ratios and logistic regression When a logistic regression is calculated, the regression coefficient (b1) is the estimated increase in the log odds of the outcome per unit increase in the value of the exposure In other words, the exponential function of the regression coefficient (e b1) is the odds ratio associated with a oneunit increase in the exposure Odds ratio vs relative risk Odds ratios and relative risks are interpreted in much the same way and if and are much less than and then the odds ratio will be almost the same as the relative risk In some sense the relative risk is a more intuitive measure of effect size Note that the choice is only for prospective studies were the distinction
Incoming Term: log odds vs odds ratio, convert log odds to odds ratio, how to say odds ratio, is a higher odds ratio better,



